Heun2#
- class brainpy.integrators.ode.Heun2(f, var_type=None, dt=None, name=None, show_code=False, state_delays=None, neutral_delays=None)[source]#
Heun’s method for ODEs.
This method is named after Karl Heun [1]. It is also known as the explicit trapezoid rule, improved Euler’s method, or modified Euler’s method.
Given ODEs with a given initial value,
\[y'(t) = f(t,y(t)), \qquad y(t_0)=y_0,\]the two-stage Heun’s method is formulated as:
\[\tilde{y}_{n+1} = y_n + h f(t_n,y_n)\]\[y_{n+1} = y_n + \frac{h}{2}[f(t_n, y_n) + f(t_{n+1},\tilde{y}_{n+1})],\]where \(h\) is the step size and \(t_{n+1}=t_n+h\).
Therefore, the Butcher tableau of the two-stage Heun’s method is:
\[\begin{split}\begin{array}{c|cc} 0.0 & 0.0 & 0.0 \\ 1.0 & 1.0 & 0.0 \\ \hline & 0.5 & 0.5 \end{array}\end{split}\]Geometric interpretation
In the
brainpy.integrators.ode.midpoint(), we have already known Euler method has big estimation error because it uses the line tangent to the function at the beginning of the interval \(t_n\) as an estimate of the slope of the function over the interval \((t_n, t_{n+1})\).In order to address this problem, Heun’s Method considers the tangent lines to the solution curve at both ends of the interval (\(t_n\) and \(t_{n+1}\)), one (\(f(t_n, y_n)\)) which underestimates, and one (\(f(t_{n+1},\tilde{y}_{n+1})\), approximated using Euler’s Method) which overestimates the ideal vertical coordinates. The ideal point lies approximately halfway between the erroneous overestimation and underestimation, the average of the two slopes.
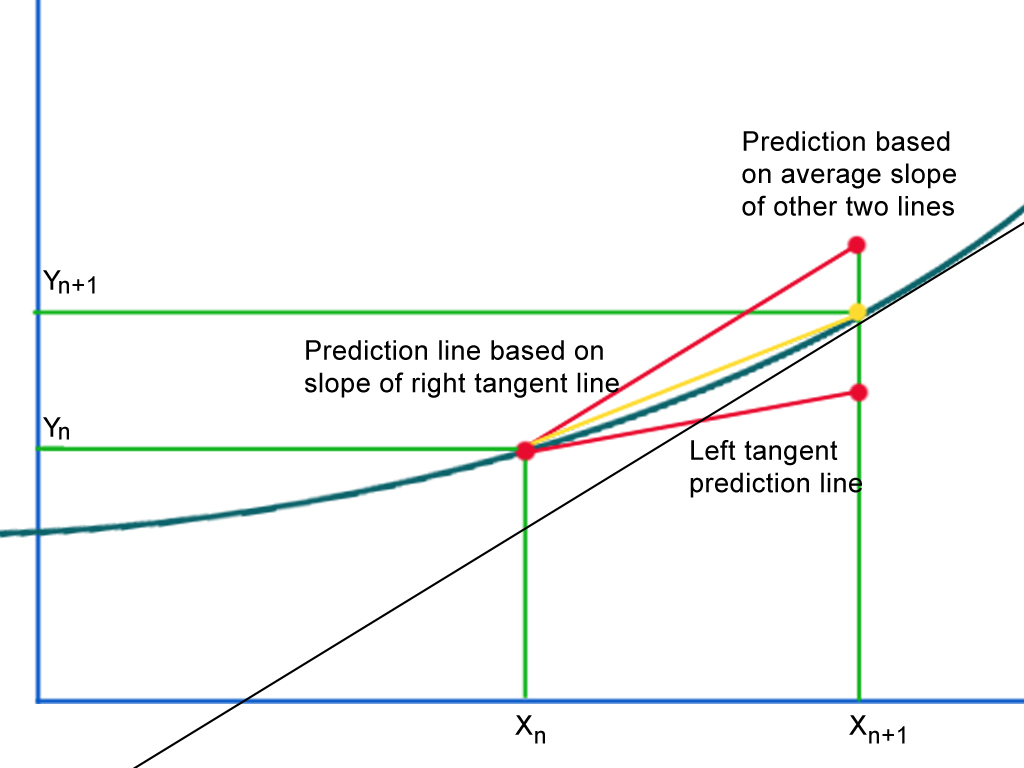\[\begin{split}\begin{aligned} {\text{Slope}}_{\text{left}}=&f(t_{n},y_{n}) \\ {\text{Slope}}_{\text{right}}=&f(t_{n}+h,y_{n}+hf(t_{n},y_{n})) \\ {\text{Slope}}_{\text{ideal}}=&{\frac {1}{2}}({\text{Slope}}_{\text{left}}+{\text{Slope}}_{\text{right}}) \end{aligned}\end{split}\]References