Concept 1: Object-oriented Transformation

Concept 1: Object-oriented Transformation#

Most computation in BrainPy relies on JAX. JAX has provided wonderful transformations, including differentiation, vecterization, parallelization and just-in-time compilation, for Python programs. If you are not familiar with it, please see its documentation.

However, JAX only supports functional programming, i.e., transformations for Python functions. This is not what we want. Brain Dynamics Modeling need object-oriented programming.

To meet this requirement, BrainPy defines the interface for object-oriented (OO) transformations. These OO transformations can be easily performed for any Python objects.

In this section, let’s talk about the BrainPy concept of object-oriented transformations.

import brainpy as bp
import brainpy.math as bm

bm.set_platform('cpu')

bp.__version__

'2.4.0'

A simple example#

Before diving into a real example, let’s illustrate the OO transformation concept using a simple case.

class Example:
    def __init__(self):
        self.static = 0
        self.dyn = bm.Variable(bm.ones(1))

    @bm.cls_jit  # JIT compiled function
    def update(self, inp):
        self.dyn.value = self.dyn * inp + self.static

example = Example()

To use OO transformations provided in BrainPy, we should keep three things in mind.

1, All dynamically changed variables should be declared as

instance of brainpy.math.Variable, (like self.dyn)
or the function argument, (like inp)

example.update(1.)
example.dyn

Variable(value=DeviceArray([1.]), dtype=float32)

example.update(2.)
example.dyn

Variable(value=DeviceArray([2.]), dtype=float32)

2, Other variables will be compiled as the constants during OO transformations. Changes made on these non-Variable or non-Argument will not show any impact after the function compiled.

example.static = 100.  # not work
example.update(1.)
example.dyn

Variable(value=DeviceArray([2.]), dtype=float32)

3, All OO transformations provided in BrainPy can be obtained from our API documentation. Simply speaking, these OO transformations include:

automatic differentiation transformations
just-in-time compilations
control flow transformations
…

A complex example: Training a network#

With the simple understanding of how OO transformations work, we can train a neural network model using the these transformations .

In this training case, we want to teach the neural network to correctly classify a random array as two labels (True or False). That is, we have the training data:

num_in = 100
num_sample = 256
X = bm.random.rand(num_sample, num_in)
Y = (bm.random.rand(num_sample) < 0.5).astype(float)

We use a two-layer feedforward network:

class Linear(bp.BrainPyObject):
    def __init__(self, n_in, n_out):
        super().__init__()
        self.num_in = n_in
        self.num_out = n_out
        init = bp.init.XavierNormal()
        self.W = bm.Variable(init((n_in, n_out)))
        self.b = bm.Variable(bm.zeros((1, n_out)))

    def __call__(self, x):
        return x @ self.W + self.b


net = bp.Sequential(Linear(num_in, 20),
                    bm.relu,
                    Linear(20, 2))
print(net)

Sequential(
  [0] <__main__.Linear object at 0x0000020636E171C0>
  [1] relu
  [2] <__main__.Linear object at 0x0000020636D867C0>
)

Here, we use a supervised learning training paradigm.

class Trainer(object):
    def __init__(self, net):
        self.net = net
        self.grad = bm.grad(self.loss, grad_vars=net.vars(), return_value=True)
        self.optimizer = bp.optim.SGD(lr=1e-2, train_vars=net.vars())

    @bm.cls_jit(inline=True)
    def loss(self):
        # shuffle the data
        key = bm.random.split_key()
        x_data = bm.random.permutation(X, key=key)
        y_data = bm.random.permutation(Y, key=key)
        # prediction
        predictions = net(dict(), x_data)
        # loss
        l = bp.losses.cross_entropy_loss(predictions, y_data)
        return l

    @bm.cls_jit
    def train(self):
        grads, l = self.grad()
        self.optimizer.update(grads)
        return l

trainer = Trainer(net)

for i in range(1, 4001):
    ls = trainer.train()
    if i % 400 == 0:
        print(f'Train {i} epoch, loss = {ls:.4f}')

Train 400 epoch, loss = 0.6190
Train 800 epoch, loss = 0.5688
Train 1200 epoch, loss = 0.5214
Train 1600 epoch, loss = 0.4776
Train 2000 epoch, loss = 0.4381
Train 2400 epoch, loss = 0.4020
Train 2800 epoch, loss = 0.3669
Train 3200 epoch, loss = 0.3335
Train 3600 epoch, loss = 0.3024
Train 4000 epoch, loss = 0.2737

In the above example, we have seen classical elements in a neural network training, such as

net: neural network
loss: loss function
grad: gradient function
optimizer: parameter optimizer
train: training step

`Variable` and `BrainPyObject`#

Although OO transformations in BrainPy do not explicitly require BrainPyObject, defining a class as a subclass of BrainPyObject will gain many advantages.

BrainPyObject can be viewed as a container which contains all needed Variable for our computation.

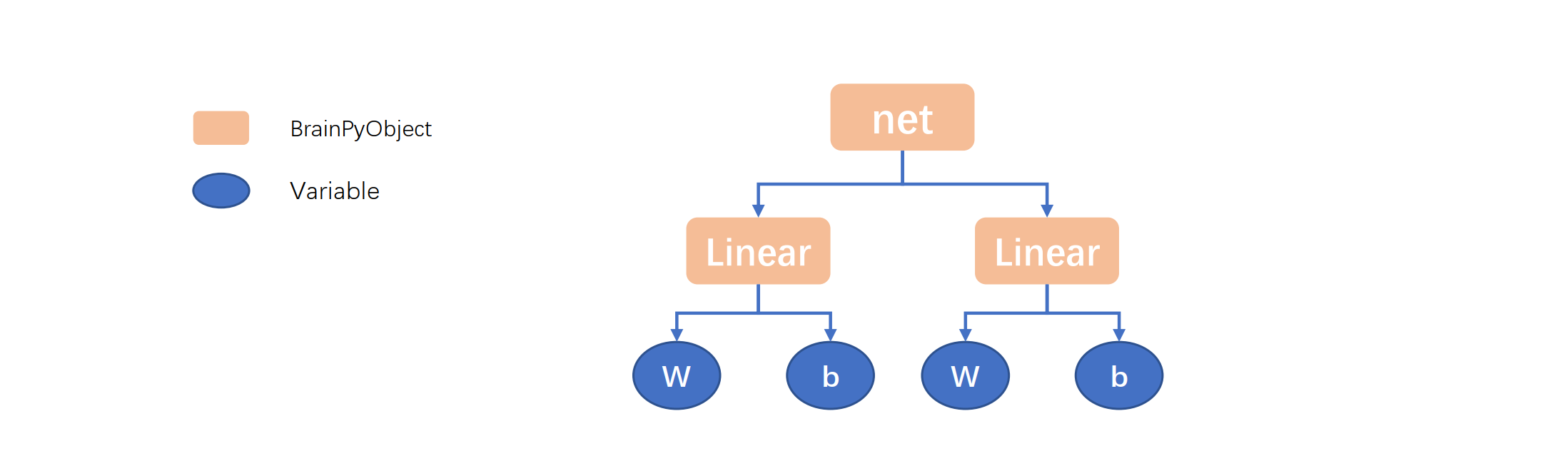
In the above example, Linear object has two Variable: W and b. The net we defined is further composed of two Linear objects. We can expect that four variables can be retrieved from it.

net.vars().keys()

dict_keys(['Linear0.W', 'Linear0.b', 'Linear1.W', 'Linear1.b'])

An important question is, how to define Variable in a BrainPyObject so that we can retrieve all of them?

Actually, all Variable instance which can be accessed by self. attribue can be retrived from a BrainPyObject recursively. No matter how deep the composition of BrainPyObject, once BrainPyObject instance and their Variable instances can be accessed by self. operation, all of them will be retrieved.

class SuperLinear(bp.BrainPyObject):
    def __init__(self, ):
        super().__init__()
        self.l1 = Linear(10, 20)
        self.v1 = bm.Variable(3)
        
sl = SuperLinear()

# retrieve Variable
sl.vars().keys()

dict_keys(['SuperLinear0.v1', 'Linear2.W', 'Linear2.b'])

# retrieve BrainPyObject
sl.nodes().keys()

dict_keys(['SuperLinear0', 'Linear2'])

However, we cannot access the BrainPyObject or Variable which is in a Python container (like tuple, list, or dict). For this case, we can use brainpy,math.NodeList or brainpy.math.VarList:

class SuperSuperLinear(bp.BrainPyObject):
    def __init__(self):
        super().__init__()
        self.ss = bm.NodeList([SuperLinear(), SuperLinear()])
        self.vv = bm.VarList([bm.Variable(3)])

ssl = SuperSuperLinear()
print(ssl.vars().keys())
print(ssl.nodes().keys())

dict_keys(['SuperSuperLinear0.vv-0', 'SuperLinear1.v1', 'SuperLinear2.v1', 'Linear3.W', 'Linear3.b', 'Linear4.W', 'Linear4.b'])
dict_keys(['SuperSuperLinear0', 'SuperLinear1', 'SuperLinear2', 'Linear3', 'Linear4'])

Concept 1: Object-oriented Transformation

Contents

Concept 1: Object-oriented Transformation#

A simple example#

A complex example: Training a network#

Variable and BrainPyObject#

`Variable` and `BrainPyObject`#