brainpy.math.surrogate.squarewave_fourier_series

brainpy.math.surrogate.squarewave_fourier_series(x, n=2, t_period=8.0)

Judge spiking state with a squarewave fourier series.

If origin=False, computes the forward function:

\[\begin{split}g(x) = \begin{cases} 1, & x \geq 0 \\ 0, & x < 0 \\ \end{cases}\end{split}\]

If origin=True, computes the original function:

\[g(x) = 0.5 + \frac{1}{\pi}*\sum_{i=1}^n {\sin\left({(2i-1)*2\pi}*x/T\right) \over 2i-1 }\]

Backward function:

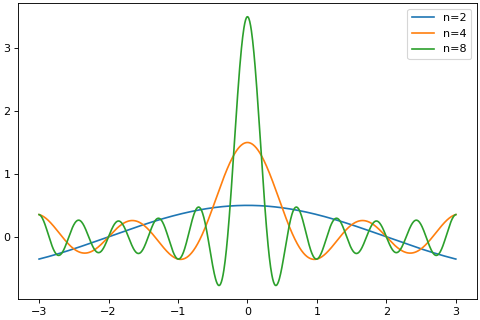
\[g'(x) = \sum_{i=1}^n\frac{4\cos\left((2 * i - 1.) * 2\pi * x / T\right)}{T}\]

>>> import brainpy as bp
>>> import brainpy.math as bm
>>> import matplotlib.pyplot as plt
>>> bp.visualize.get_figure(1, 1, 4, 6)
>>> xs = bm.linspace(-3, 3, 1000)
>>> for n in [2, 4, 8]:
>>>   f = bm.surrogate.SquarewaveFourierSeries(n=n)
>>>   grads1 = bm.vector_grad(f)(xs)
>>>   plt.plot(bm.as_numpy(xs), bm.as_numpy(grads1), label=f'n={n}')
>>> plt.legend()
>>> plt.show()

(Source code, png, hires.png, pdf)

Parameters:

• x (jax.Array, Array) – The input data.

• n (int) –

• t_period (float) –

Returns:

out – The spiking state.

Return type:

jax.Array