Dedicated Operators

Dedicated Operators#

In the previous section, we have learned that BrainPy offers brainpy.math.array that support common NumPy-like operations, which brings great convenience to users familiar with NumPy. NumPy-like operations, however, does not always apply to brain dynamics modeling. As one may recognize, the most costive computation in brain dynamics modeling lies in synaptic computation, as it involves the connection between two neuron groups. Two of the most salient features of synaptic computation are:

Sparse connection: neuron-neuron connection in most brain regions is sparse.
Event-driven synaptic transmission: synaptic transmission happens only when the presynaptic neurons fire.

If we stick to array-related operations, there rise some problems making the computation extremely inefficient:

Because of sparse connection, keeping using traditional array operations (e.g., matrix multiplication) will cause a huge waste in memory allocation and computation.
Because of event-driven synaptic transmission, only a small proportion of presynaptic neurons are activated at a time, resulting in sparse transmission from pre- to post-synaptic neuron populations. Traditional array operations will compute the transmission based on the connection from all presynaptic neurons to their postsynaptic elements, unable to exclude those inactive neurons and to avoid redundant computation.

To show these two features more intuitively, here is an illustration of computing postsynaptic inputs from presynaptic events and their connection:

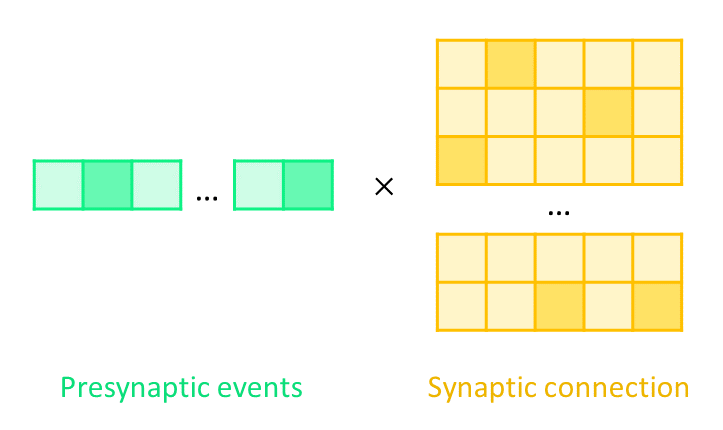
In essence, the synaptic computation is the multiplication of a vector and a matrix. If presynaptic events and synaptic connection are both sparse, it will be extremely wasteful to use NumPy-like matrix multiplication.

In this section, we are introducing some decicated operators for sparse and event-driven computation to make brain dynamics modeling much more efficient.

import brainpy as bp
import brainpy.math as bm

bm.set_platform('cpu')

Operators for sparse synaptic computation#

Firstly, let’s consider the situation when the synaptic connection is sparse. Here is an example of the connection between two groups of neurons:

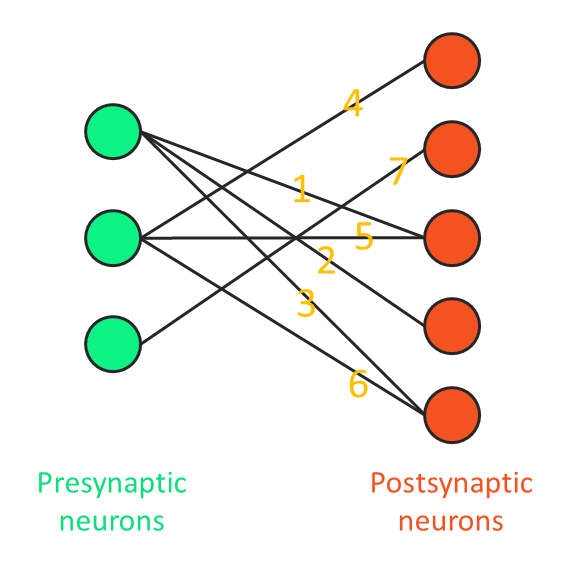
The yellow numbers on the connection lines indicate the connection weights. We can convert the connection pattern into a connection matrix, where each row represents a presynaptic neuron and each column represents a postsynaptic neuron:

conn_mat = bm.array([[0, 0, 1, 2, 3], 
                     [4, 0, 5, 0, 6], 
                     [0, 7, 0, 0, 0]]).astype(float)
conn_mat

Array(value=Array([[0., 0., 1., 2., 3.],
                   [4., 0., 5., 0., 6.],
                   [0., 7., 0., 0., 0.]]),
      dtype=float32)

Assume that at a given time, presynaptic neurons are active with different values (2, 1, 3), so the postsynaptic inputs from these three presynaptic neurons can be computed as the multiplication of a vector and a sparse matrix:

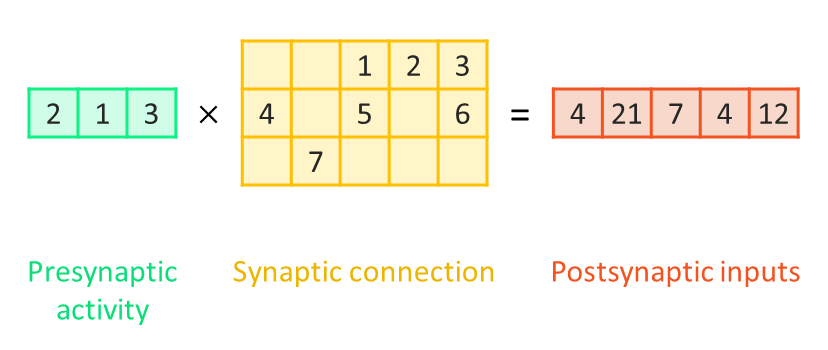
In which the presynaptic activity is displayed as a vector.

pre_activity = bm.array([2., 1., 3.])

bm.matmul(pre_activity, conn_mat)

Array(value=Array([ 4., 21.,  7.,  4., 12.]), dtype=float32)

While this multiplication is intuitive, the computation is inefficient if the connection matrix is sparse. To save memory storage and improve running efficiency, we can use other data structures to store the sparse connection without so many empty values. One of the data structures is the Compressed Sparse Row (CSR) matrix.

Simply speaking, the CSR matrix stores the connection information by three vectors: the non-zero weight values in the connection matrix, the post-synaptic neuron indices, and the corresponding presynaptic neuron pointers (users can see the pre2post connection properties in Synaptic Connections for more information). Without knowing the details, the vectors can still easily be obtained by the following operations:

data = conn_mat[bm.nonzero(conn_mat)]

# difine a connection from a connection matrix by brainpy.conn.Matconn 
connection = bp.conn.MatConn(conn_mat.value)
# obtain these properties by .require('pre2post')
indices, indptr = connection(conn_mat.shape[0], conn_mat.shape[1]).require('pre2post')

data, indices, indptr

(Array([1., 2., 3., 4., 5., 6., 7.], dtype=float32),
 Array([2, 3, 4, 0, 2, 4, 1], dtype=int32),
 Array([0, 3, 6, 7], dtype=int32))

Then we can use the dedicated operators brainpy.math.sparse.csrmv to compute the postsynaptic inputs (i.e., the product of a CSR Matrix and a Vector):

bm.sparse.csrmv(data, indices=indices, indptr=indptr, vector=pre_activity, 
                shape=conn_mat.shape, transpose=True)

Array([ 4., 21.,  7.,  4., 12.], dtype=float32)

In which the non-zero connection values, the postsynaptic indices, the presynaptic neuron pointers, the presynaptic activity, and the connection shape (a tuple of the number of pre- and post-synaptic neurons) and whether to transpose the sparse matrix are passed to the fucntion. It returns the same results, but with a higher speed if the connection is sparse (we will see the comparison of their running time shortly).

Operators for event-driven synaptic computation#

Above we have talked about the situation when the synaptic connection is sparse. What if the presynaptic events are also sparse? Theoretically, more time will be saved if we remove the redundant computation of the connection from inactive presynaptic neurons. In this condition, we can use event-driven operators in brainpy.math.event.

Assume that in the above example, the presynaptic neuron 0 and 1 are firing and neuron 2 is inactive (now their acitivities are represented by boolean values):

event = bm.array([True, True, False])

The multiplication of the event vector and the connection matrix now becomes:

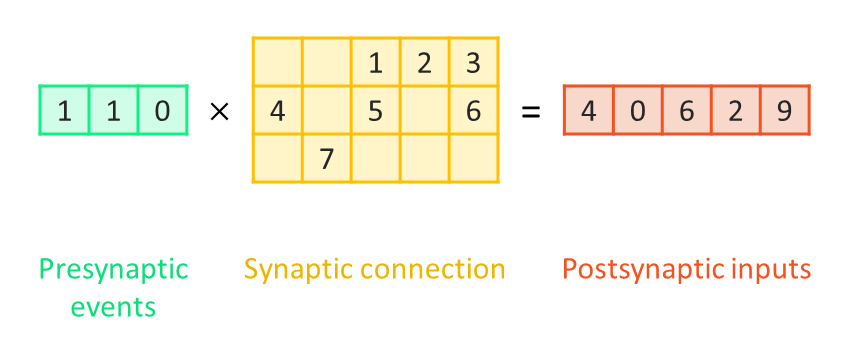
Of course we can use traditional matrix multiplication operators and the brainpy.math.sparse.csrmv operator for computation. However, by simply changing brainpy.math.sparse.csrmv to brainpy.math.event.csrmv, we can achieve event-driven synaptic computation and become even faster:

bm.event.csrmv(data, indices=indices, indptr=indptr, events=event, 
               shape=conn_mat.shape, transpose=True)

Array([4., 0., 6., 2., 9.], dtype=float32)

Note that the parameter vector in brainpy.math.sparse.csrmv is revised to a boolean-type array events in brainpy.math.event.csrmv.

Now let’s compare the efficiency of traditional matrix operators, brainpy.math.sparse.csrmv, and brainpy.math.event.csrmv. To show a significant difference, a much larger network is used.

from timeit import default_timer

pre_num, post_num = 15000, 10000  # network size

event = bm.random.bernoulli(p=0.15, size=pre_num)  # 15% of presynaptic neurons are active

The traditional matrix operator is tested first:

# generate the weight matrix
start = default_timer()

connection_weights = bm.random.uniform(size=(pre_num, post_num))
connection_weights[connection_weights < 0.8] = 0.  # sparse connection: 20%

duration = default_timer() - start

print('time spent for weight matrix generation: {} s'.format(duration))

time spent for weight matrix generation: 4.558527099999992 s

# traditional matrix operator
start = default_timer()

post = bm.matmul(event, connection_weights)

duration = default_timer() - start

print('time spent for synaptic computation: {} s'.format(duration))

time spent for synaptic computation: 0.03688780000001657 s

Note that to exclude the time for JIT compilation, the code was run twice and the second result is displayed. Though the running time for brainpy.math.matmul is acceptable, a huge amount of time is spent on weight matrix generation, which is extremely inefficient.

For sparse matrix, using the CSR matrix structure to store data and to compute the product is more efficient:

# generate connection and store it in a CSR matrix
start = default_timer()

# define a connection with fixed connection probability by brainpy.conn.FixedProb
connection = bp.conn.FixedProb(prob=0.2)
# obtain these properties by .require('pre2post')
indices, indptr = connection(pre_num, post_num).require('pre2post')
data = bm.random.uniform(size=indices.shape)

duration = default_timer() - start

print('time spent for connection generation: {} s'.format(duration))

time spent for connection generation: 1.61494689999995 s

# dedicated sparse operator
pre_activity = event.astype(float)

start = default_timer()

post = bm.sparse.csrmv(data, indices=indices, indptr=indptr, vector=pre_activity, 
                       shape=(pre_num, post_num), transpose=True)

duration = default_timer() - start

print('time spent for synaptic computation: {} s'.format(duration))

time spent for synaptic computation: 0.0551689000000124 s

Due to a large number of inactive presynaptic neurons, sparse connection matrix is not the optimal solution until event-driven computation is involved:

start = default_timer()

post = bm.event.csrmv(data, indices=indices, indptr=indptr, events=event, 
                      shape=(pre_num, post_num), transpose=True)

duration = default_timer() - start

print('time spent for synaptic computation: {} s'.format(duration))

time spent for synaptic computation: 0.015149300000018684 s

Now the running time is significantly lower than the other two operators.

To summarize, for synaptic computation with a sparse connection matrix, operators in brainpy.math.sparse are recommended. Furthermore, if the presynaptic activity is also sparse, operators in brainpy.math.event are better choices.

Even faster synaptic computation with specific connection patterns#

The synaptic computation, the multiplication of a vector and a sparse matrix, though impressively accelerated by the event-driven and sparse operators in BrainPy, can be improved even further in some situations.

When building a brain model, we often encounter situations like this:

each presynaptic neuron is randomly connected with postsynaptic neurons in a fixed probability, and
the connection weights obey certain rules, such as being a constant value or generated from a normal distribution.

One solution is to generate the random connection and the corresponding weights and store them in a sparse matrix, and then use BrainPy’s dedicated operators for synaptic computation. To further improve the performance, BrainPy provides another solution, which is to generate the connection information during synaptic computation, thusing saving the space to store connection and the time to interact with memory.

Currently, BrainPy provides two types of such operators, one of which is regular and the other is event-driven. They are contained in brainpy.math.jitconn, which means the random connection is just-in-time generated during computation. Let’s take as an example the event-driven operator to compute synaptic transmission when 1. the connection matrix is randomly generated with a fixed probability and 2. the conection weights are generated from a normal distribution.

Firstly, let’s think of how this is achieved without any dedicated operators. Below are the related parameters:

pre_num, post_num = 50000, 10000  # network size
conn_prob = 0.1  # connection probability
w_mu, w_sigma = 0.5, 1.  # parameters of the normal distribution

And a vector representing presynaptic acitivty is also needed:

event = bm.random.bernoulli(p=0.2, size=pre_num)  # 20% of presynaptic neurons release spikes

To obtain a random connection with fixed probability, we need to generate a bool-type connection matrix. To obtain a normally distributed weight matrix, we should also generate a weight matrix with float numbers. Then we can compute the postsynaptic inputs by multiplying the event vector and the elementwise product of the connection and the weight matrix:

start = default_timer()

# generate the connection matrix using brainpy.connect.FixedProb
conn = bp.connect.FixedProb(prob=conn_prob)(pre_num, post_num)
conn_matrix = conn.require('conn_mat')

# generate the weight matrix
weight_matrix = bm.random.normal(loc=w_mu, scale=w_sigma, size=(pre_num, post_num))

# compute the product
post = bm.matmul(event, weight_matrix * conn_matrix)

duration = default_timer() - start

print('time spent: {} s'.format(duration))

time spent: 11.050910799999997 s

The total running time is about 10 seconds. Now let’s try to use brainpy.math.event.csrmv to see how much improvement it makes.

start = default_timer()

# generate the connection with the pre2post structure
conn = bp.connect.FixedProb(prob=conn_prob)(pre_num, post_num)
indices, indptr = conn.require('pre2post')

# generate the weight matrix
weights = bm.random.normal(loc=w_mu, scale=w_sigma, size=indices.shape[0])

# compute the event-driven synaptic summation
post = bm.event.csrmv(weights, indices, indptr, event, shape=(pre_num, post_num), 
                      transpose=True)

duration = default_timer() - start

print('time spent: {} s'.format(duration))

time spent: 4.693945999999983 s

Now the running time halves, but it is still unsatisfactory. Then we try to use a new operator, brainpy.math.jitconn.event_mv_prob_normal, which does not generate the connection and weights explicitly but achieves it while doing the matrix multiplication.

start = default_timer()

# the connection is generated during computation, 
# so the entire connection information is not required to be stored or accessed
post = bm.jitconn.event_mv_prob_normal(event, w_mu=w_mu, w_sigma=w_sigma, conn_prob=conn_prob, 
                                       shape=(pre_num, post_num), transpose=True)

duration = default_timer() - start

print('time spent: {} s'.format(duration))

time spent: 0.0062690999999404085 s

Surprisingly, the time spent is much less than the privous operations! Therefore, users are recommended to use these operators to multiply a vector and a sparse matrix if the situation is as follows:

Use brainpy.math.jitconn.mv_prob_homo(), if the connection is of fixed probability, and the connection weight is a constant (a single value).
Use brainpy.math.jitconn.mv_prob_uniform(), if the connection is of fixed probability, and the connection weight is sampled from a uniform distribution.
Use brainpy.math.jitconn.mv_prob_normal(), if the connection is of fixed probability, and the connection weight is sampled from a normal distribution.

Besides, there are three corresponding event-driven operators, brainpy.math.jitconn.event_mv_prob_homo(), brainpy.math.jitconn.event_mv_prob_uniform(), and brainpy.math.jitconn.event_mv_prob_normal(), for event-driven synaptic computation.

Dedicated Operators

Contents

Dedicated Operators#

Operators for sparse synaptic computation#

Operators for event-driven synaptic computation#

Even faster synaptic computation with specific connection patterns#