Joint Differential Equations#
In a dynamical system, there may be multiple variables that change dynamically over time. Sometimes these variables are interconnected, and updating one variable requires others as the input. For example, in the widely known Hodgkin–Huxley model, the variables \(V\), \(m\), \(h\), and \(n\) are updated synchronously and interdependently (please refer to Building Neuron Modelsfor details). To achieve higher integral accuracy, it is recommended to use brainpy.JointEq to jointly solving interconnected differential equations.
import brainpy as bp
brainpy.JointEq#
brainpy.JointEq is used to merge individual but interconnected differential equations into a single joint equation. For example, below are the two differential equations of the Izhikevich model:
a, b = 0.02, 0.20
dV = lambda V, t, u, Iext: 0.04 * V * V + 5 * V + 140 - u + Iext
du = lambda u, t, V: a * (b * V - u)
Where updating \(V\) requires \(u\) as the input, and updating \(u\) requires \(V\) as the input. The joint equation can be defined as:
joint_eq = bp.JointEq(dV, du)
brainpy.JointEq receives only one argument named eqs, which can be a list or tuple containing multiple differential equations. Then it can be packed into a numarical integrator that solves the equation with a specified method, just as what can be done to any individual differential equation.
itg = bp.odeint(joint_eq, method='rk2')
There are several requirements for defining a joint equation:
Every individual differential equation should follow the format of defining a ODE or SDE funtion in BrainPy. For example, the arguments before
tdenote the dynamical variables and arguments aftertdenote the parameters.The same variable in different equations should have the same name. Different variables should named differently.
Note that brainpy.JointEq supports make nested JointEq, which means the instance of JointEq can be an element to compose a new JointEq.
Why use brainpy.JointEq?#
Users may be confused with the function of brainpy.JointEq, because multiple differential equations can be written in a single function:
def diff(V, u, t, Iext):
dV = 0.04 * V * V + 5 * V + 140 - u + Iext
du = a * (b * V - u)
return dV, du
itg_V_u = bp.odeint(diff, method='rk2')
or simply packed into interators separately:
int_V = bp.odeint(dV, method='rk2')
int_u = bp.odeint(du, method='rk2')
To illusrate the difference between joint and separate differential equations, let’s dive into the differential codes of these two types of equations.
If we make numerical solver for each derivative function, they will be solved independently:
import brainpy as bp
bp.odeint(dV, method='rk2', show_code=True)
def brainpy_itg_of_ode4(V, t, u, Iext, dt=0.1):
dV_k1 = f(V, t, u, Iext)
k2_V_arg = V + dt * dV_k1 * 0.6666666666666666
k2_t_arg = t + dt * 0.6666666666666666
dV_k2 = f(k2_V_arg, k2_t_arg, u, Iext)
V_new = V + dV_k1 * dt * 0.25 + dV_k2 * dt * 0.75
return V_new
{'f': <function <lambda> at 0x000001CD0E12B040>}
<brainpy._src.integrators.ode.explicit_rk.RK2 at 0x1cd0f688af0>
As is shown in the output code, the variable \(V\) is integrated twice by the RK2 method. For the second differential value dV_k2, the updated value of \(V\) (k2_V_arg) and original \(u\) are used to calculate the differential value. This will generate a tiny error, since the values of \(V\) and \(u\) are taken at different times.
To eliminate this error, the differential equation of \(V\) and \(u\) should be solved jointly through brainpy.JointEq:
eq = bp.JointEq(dV, du)
bp.odeint(eq, method='rk2', show_code=True)
def brainpy_itg_of_ode5_joint_eq(V, u, t, Iext, dt=0.1):
dV_k1, du_k1 = f(V, u, t, Iext)
k2_V_arg = V + dt * dV_k1 * 0.6666666666666666
k2_u_arg = u + dt * du_k1 * 0.6666666666666666
k2_t_arg = t + dt * 0.6666666666666666
dV_k2, du_k2 = f(k2_V_arg, k2_u_arg, k2_t_arg, Iext)
V_new = V + dV_k1 * dt * 0.25 + dV_k2 * dt * 0.75
u_new = u + du_k1 * dt * 0.25 + du_k2 * dt * 0.75
return V_new, u_new
{'f': <brainpy._src.integrators.joint_eq.JointEq object at 0x000001CD0F6810A0>}
<brainpy._src.integrators.ode.explicit_rk.RK2 at 0x1cd0f6814c0>
It is shown in this output code that second differential values of \(v\) and \(u\) are calculated by using the updated values (k2_V_arg and k2_u_arg) at the same time. This will result in a more accurate integral.
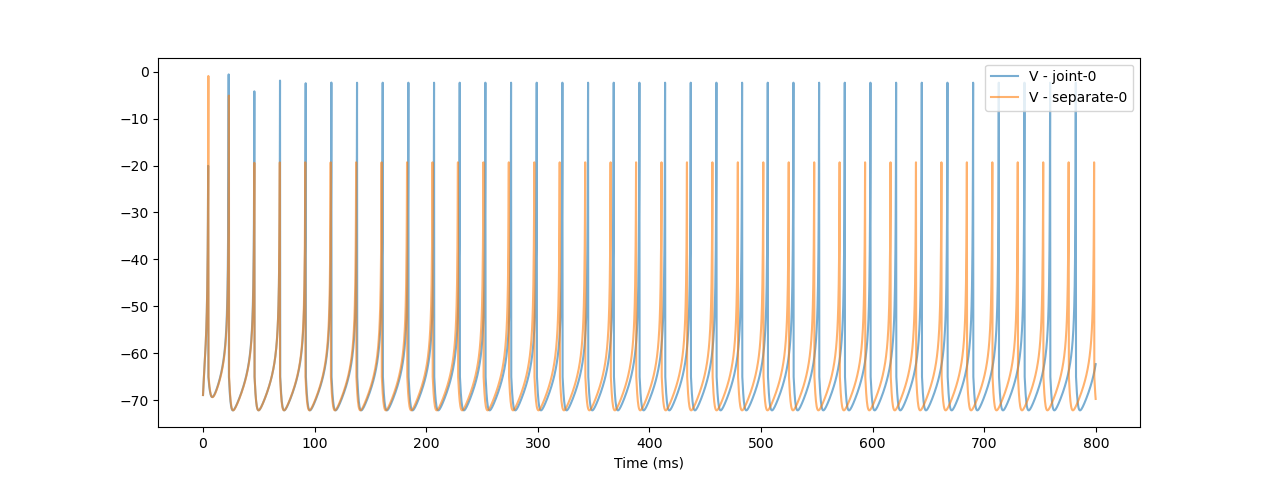
The figure below compares the simulation results of the Izhikevich model using joint and separate differential equations (\(dt = 0.2 ms\)). It is shown that as the simulation time increases, the integral error becomes greater.