Inputs Construction

@Chaoming Wang @Xiaoyu Chen

In this section, we are going to talk about stimulus inputs.

import brainpy as bp
import brainpy.math as bm

bp.__version__

'2.4.0'

Input construction functions

Like electrophysiological experiments, model simulation also needs various kind of inputs. BrainPy provide several convenient input functions to help users construct input currents.

1. brainpy.inputs.section_input()

brainpy.inputs.section_input() is an updated function of previous brainpy.inputs.constant_input() (see below).

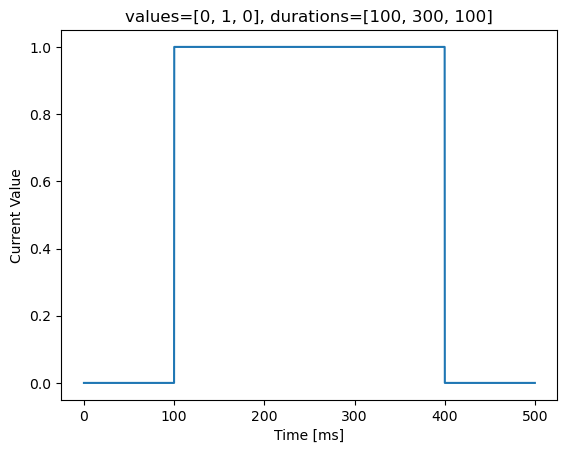
Sometimes, we need input currents with different values in different periods. For example, if you want to get an input that is 0 in the first 100 ms, 1 in the next 300 ms, and 0 again from the last 100 ms, you can define:

current1, duration = bp.inputs.section_input(values=[0, 1., 0.],
                                             durations=[100, 300, 100],
                                             return_length=True,
                                             dt=0.1)

WARNING:absl:No GPU/TPU found, falling back to CPU. (Set TF_CPP_MIN_LOG_LEVEL=0 and rerun for more info.)

Where values receive a list/arrray of the current values in each section and durations receives a list/array of the duration of each section. The function returns a tensor as the current, the length of which is duration\(/\mathrm{d}t\) (if not specified, \(\mathrm{d}t=0.1 \mathrm{ms}\)). We can visualize the current input by:

import numpy as np
import matplotlib.pyplot as plt

def show(current, duration, title):
    ts = np.arange(0, duration, bm.get_dt())
    plt.plot(ts, current)
    plt.title(title)
    plt.xlabel('Time [ms]')
    plt.ylabel('Current Value')
    plt.show()

show(current1, duration, 'values=[0, 1, 0], durations=[100, 300, 100]')

2. brainpy.inputs.constant_input()

brainpy.inputs.constant_input() function helps users to format constant currents in several periods.

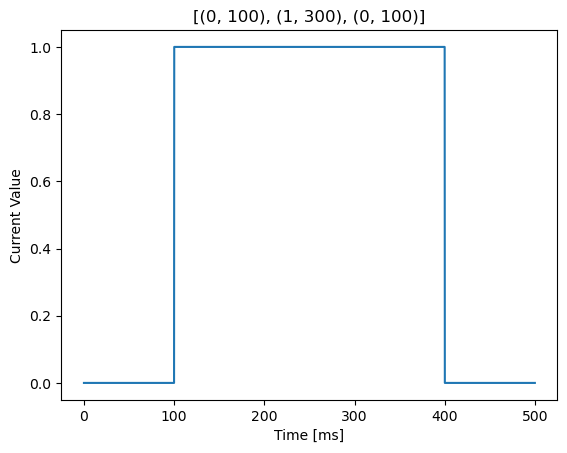
We can generate the above input current with constant_input() by:

current2, duration = bp.inputs.constant_input([(0, 100), (1, 300), (0, 100)])

Where each tuple in the list contains the value and duration of the input in this section.

show(current2, duration, '[(0, 100), (1, 300), (0, 100)]')

3. brainpy.inputs.spike_input()

brainpy.inputs.spike_input() constructs an input containing a series of short-time spikes. It receives the following settings:

• sp_times : The spike time-points. Must be an iterable object. For example, list, tuple, or arrays.

• sp_lens : The length of each point-current, mimicking the spike durations. It can be a scalar float to specify the unified duration. Or, it can be list/tuple/array of time lengths with the length same with sp_times.

• sp_sizes : The current sizes. It can be a scalar value. Or, it can be a list/tuple/array of spike current sizes with the length same with sp_times.

• duration : The total current duration.

• dt : The time step precision. The default is None (will be initialized as the default dt step).

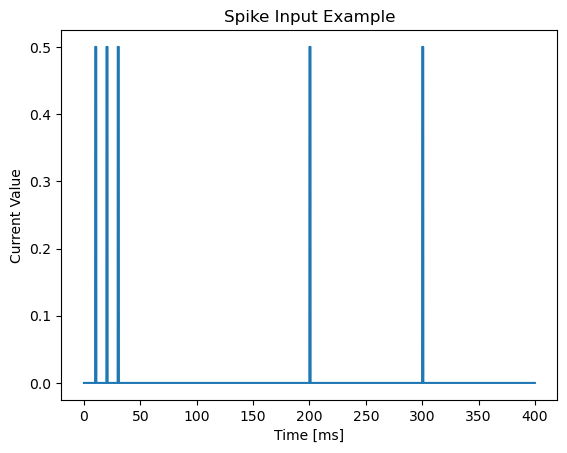
For example, if you want to generate a spike train at 10 ms, 20 ms, 30 ms, 200 ms, 300 ms, where each spike lasts 1 ms and the average value for each spike is 0.5, then you can define the current by:

current3 = bp.inputs.spike_input(
    sp_times=[10, 20, 30, 200, 300],
    sp_lens=1.,  # can be a list to specify the spike length at each point
    sp_sizes=0.5,  # can be a list to specify the spike current size at each point
    duration=400.)

show(current3, 400, 'Spike Input Example')

4. brainpy.inputs.ramp_input()

brainpy.inputs.ramp_input() mimics a ramp or a step current to the input of the circuit. It receives the following settings:

• c_start : The minimum (or maximum) current size.

• c_end : The maximum (or minimum) current size.

• duration : The total duration.

• t_start : The ramped current start time-point.

• t_end : The ramped current end time-point. Default is the None.

• dt : The current precision.

We illustrate the usage of brainpy.inputs.ramp_input() by two examples.

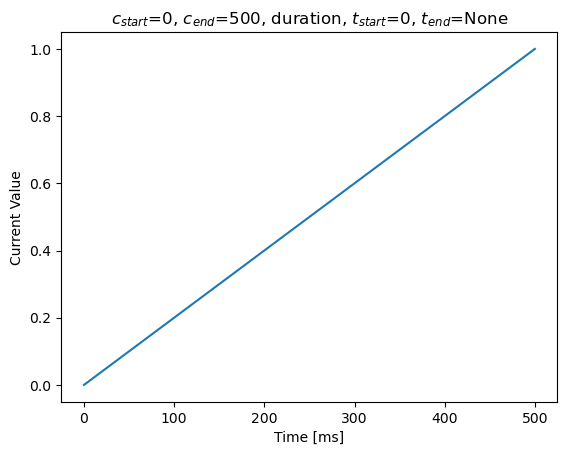
In the first example, we increase the current size from 0. to 1. between the start time (0 ms) and the end time (500 ms).

duration = 500
current4 = bp.inputs.ramp_input(0, 1, duration)

show(current4, duration, r'$c_{start}$=0, $c_{end}$=%d, duration, '
                        r'$t_{start}$=0, $t_{end}$=None' % (duration))

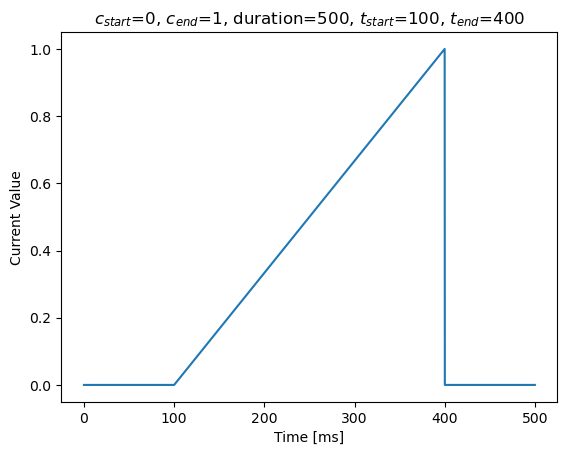
In the second example, we increase the current size from 0. to 1. from the 100 ms to 400 ms.

duration, t_start, t_end = 500, 100, 400
current5 = bp.inputs.ramp_input(0, 1, duration, t_start, t_end)

show(current5, duration, r'$c_{start}$=0, $c_{end}$=1, duration=%d, '
                        r'$t_{start}$=%d, $t_{end}$=%d' % (duration, t_start, t_end))

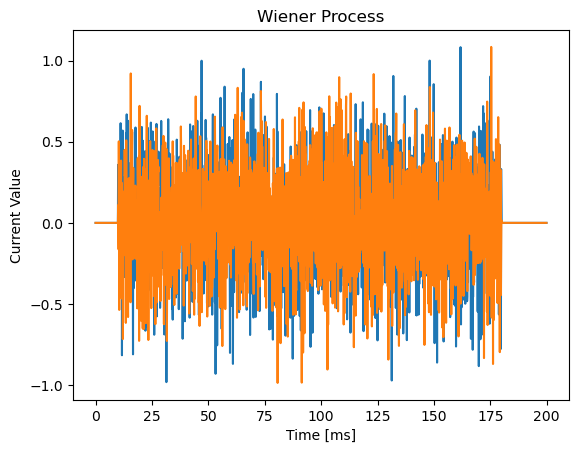
5. brainpy.inputs.wiener_process

brainpy.inputs.wiener_process() is used to generate the basic Wiener process \(dW\), i.e. random numbers drawn from \(N(0, \sqrt{dt})\).

duration = 200
current6 = bp.inputs.wiener_process(duration, n=2, t_start=10., t_end=180.)
show(current6, duration, 'Wiener Process')

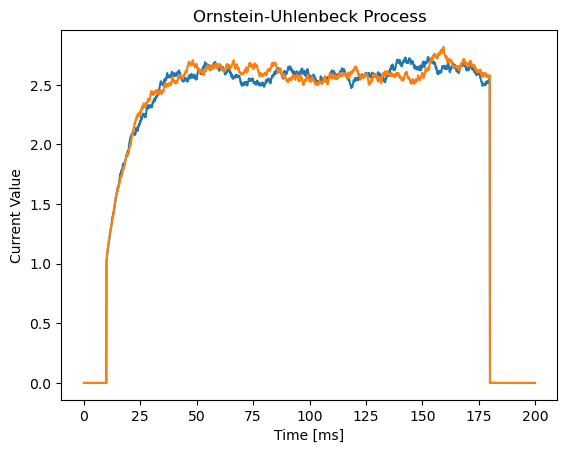
6. brainpy.inputs.ou_process

brainpy.inputs.ou_process() is used to generate the noise time series from Ornstein-Uhlenback process \(\dot{x} = (\mu - x)/\tau \cdot dt + \sigma\cdot dW\).

duration = 200
current7 = bp.inputs.ou_process(mean=1., sigma=0.1, tau=10., duration=duration, n=2, t_start=10., t_end=180.)
show(current7, duration, 'Ornstein-Uhlenbeck Process')

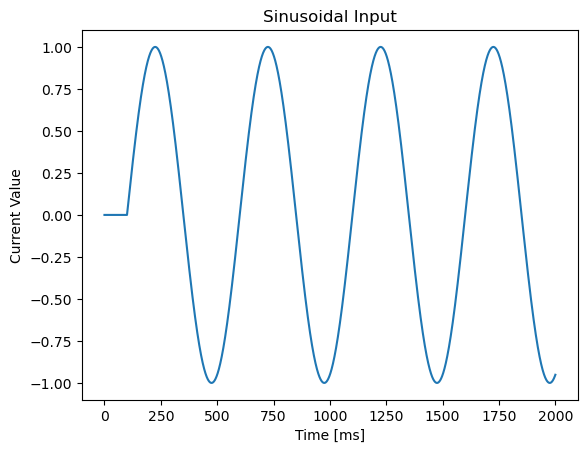
7. brainpy.inputs.sinusoidal_input

brainpy.inputs.sinusoidal_input() can help to generate sinusoidal inputs.

duration = 2000
current8 = bp.inputs.sinusoidal_input(amplitude=1., frequency=2.0, duration=duration,  t_start=100., )
show(current8, duration, 'Sinusoidal Input')

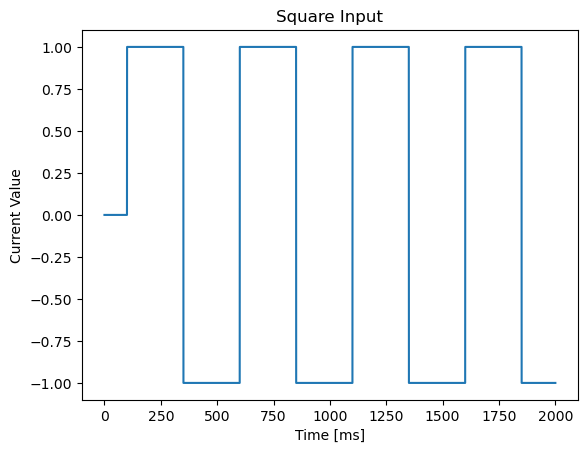
8. brainpy.inputs.square_input

brainpy.inputs.square_input() can help to generate oscillatory square inputs.

duration = 2000
current9 = bp.inputs.square_input(amplitude=1., frequency=2.0,
                                  duration=duration, t_start=100)
show(current9, duration, 'Square Input')

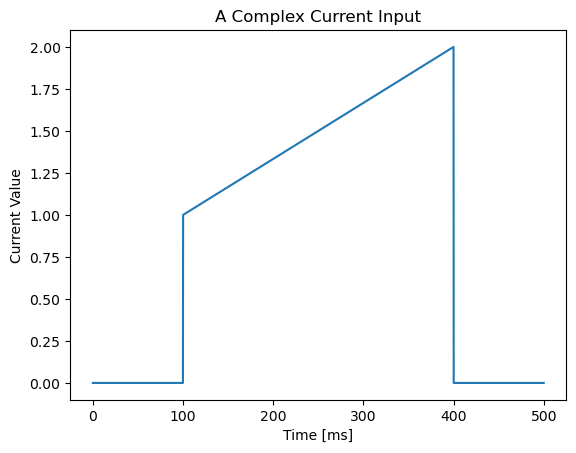
More complex inputs

Because the current input is stored as a tensor, a complex input can be realized by the combination of several simple currents.

show(current1 + current5, 500, 'A Complex Current Input')

General properties of input functions

1. Every input function receives a dt specification.

If dt is not provided, input functions will use the default dt in the whole BrainPy system.

I1 = bp.inputs.section_input(values=[0, 1, 2], durations=[10, 20, 30], dt=0.1)
I2 = bp.inputs.section_input(values=[0, 1, 2], durations=[10, 20, 30], dt=0.01)
print('I1.shape: {}'.format(I1.shape))
print('I2.shape: {}'.format(I2.shape))

I1.shape: (600,)
I2.shape: (6000,)

2. All input functions can automatically broadcast the current shapes if they are heterogenous among different periods.

For example, during period 1 we give an input with a scalar value, during period 2 we give an input with a vector shape, and during period 3 we give a matrix input value. Input functions will broadcast them to the maximum shape. For example:

current = bp.inputs.section_input(values=[0, bm.ones(10), bm.random.random((3, 10))],
                                  durations=[100, 300, 100])

current.shape

(5000, 3, 10)