brainpy.math.surrogate.soft_sign#
- brainpy.math.surrogate.soft_sign(x, alpha=1.0)[source]#
Judge spiking state with a soft sign function.
If origin=False, computes the forward function:
\[\begin{split}g(x) = \begin{cases} 1, & x \geq 0 \\ 0, & x < 0 \\ \end{cases}\end{split}\]If origin=True, computes the original function:
\[g(x) = \frac{1}{2} (\frac{\alpha x}{1 + |\alpha x|} + 1) = \frac{1}{2} (\frac{x}{\frac{1}{\alpha} + |x|} + 1)\]Backward function:
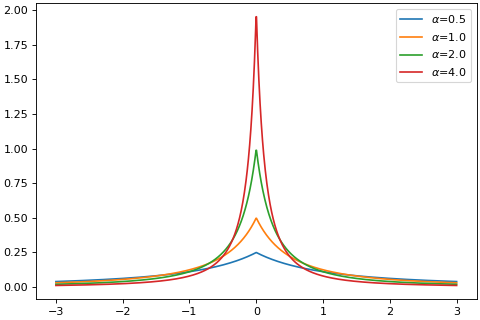
\[g'(x) = \frac{\alpha}{2(1 + |\alpha x|)^{2}} = \frac{1}{2\alpha(\frac{1}{\alpha} + |x|)^{2}}\]>>> import brainpy as bp >>> import brainpy.math as bm >>> import matplotlib.pyplot as plt >>> bp.visualize.get_figure(1, 1, 4, 6) >>> xs = bm.linspace(-3, 3, 1000) >>> for alpha in [0.5, 1., 2., 4.]: >>> grads = bm.vector_grad(bm.surrogate.soft_sign)(xs, alpha) >>> plt.plot(xs, grads, label=r'$\alpha$=' + str(alpha)) >>> plt.legend() >>> plt.show()
(
Source code,png,hires.png,pdf)